Mecanica

La física mecánica estudia el movimiento de los cuerpos.

Se divide en cinemática, estática y dinámica: 

• La cinemática estudia el movimiento de los cuerpos sin considerar la causa que produce el movimiento.

• La dinámica estudia el movimiento de los cuerpos considerando la causa que estudia el movimiento.
• La estática estudia el equilibrio de los cuerpos                                                                                            

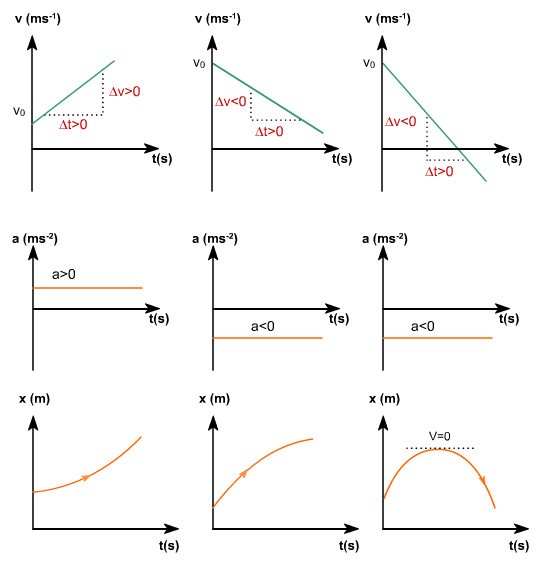
  Cinemática se divide en movimiento unidimensional y bidimensional En el primero se estudia el movimiento rectilíneo uniforme (MRU) y movimiento rectilíneo uniforme acelerado (MRUA) En el segundo, también se conoce como movimiento en el plano y se estudia el movimiento de proyectiles. Dinámica hace referencia al estudia de las leyes de Newton, las cuales son tres, la primera ley establece que todo cuerpo tiende a establecer su estado de reposo o movimiento rectilíneo uniforme en ausencia de fuerzas externas. La segunda ley se conoce como ley de causa y efecto y dice que la sumatoria de fuerzas o fuerza neta es igual a la rapidez de cambio del momento lineal. La tercera ley es la de acción y reacción que establece que toda acción tiene una reacción de igual magnitud pero en sentido opuesto La estática tiene que ver con el equilibrio de los cuerpos, los cuales deben cumplir dos condiciones; la primera se llama equilibrio de traslación y establece que la sumatoria de fuerzas que actúa sobre un cuerpo debe ser igual a cero y la segunda condición establece que la sumatoria de torques respecto a un punto debe ser igual a cero

                                                                                                                              

Movimiento

el movimiento es un cambio de la posición de un cuerpo a lo largo del tiempo respecto de un sistema de referencia.

El estudio del movimiento se puede realizar a través de la cinemática o a través de la dinámica. En función de la elección del sistema de referencia quedaran definidas las ecuaciones del movimiento, ecuaciones que determinarán la posición, la velocidad y la aceleración del cuerpo en cada instante de tiempo. Todo movimiento puede representarse y estudiarse mediante gráficas. Las más habituales son las que representan el espacio, la velocidad o la aceleración en función del tiempo.

El movimiento se refiere al cambio de ubicación en el espacio a lo largo del tiempo, tal como es medido por un observador físico. Un poco más generalmente el cambio de ubicación puede verse influido por las propiedades internas de un cuerpo o sistema físico, o incluso el estudio del movimiento en toda su generalidad lleva a considerar el cambio de dicho estado físico.

ELEMENTOS DEL MOVIMIENTO:

1. Posición del cuerpo.
2. La trayectoria
3. Espacio recorrido.
4. Desplazamiento.

Linea del tiempo

Vector

Vector

En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida por un punto del espacio donde se mide dicha magnitud, además de un módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).^1 2 3

En Matemáticas se define un vector como un elemento de un espacio vectorial, esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. 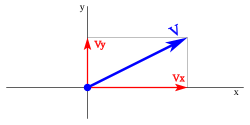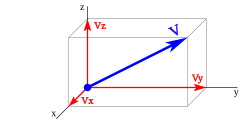Los vectores en un espacio euclídeo se pueden representar geométrica mente como segmentos de recta dirigidos («flechas») en el plano  o en el espacio .

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.

Características de un vector[editar]

Coordenadas cartesianas.

Un vector se puede definir por sus coordenadas, si el vector esta en el plano xy, se representa:

siendo sus coordenadas:

Siendo el vector la suma vectorial de sus coordenadas:

Coordenadas tridimensionales.

Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:

siendo sus coordenadas:

Si representamos el vector gráficamente podemos diferenciar la recta soporte o dirección, sobre la que se traza el vector.

El módulo o amplitud con una longitud proporcional al valor del vector.

El sentido, indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.

El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.

El nombre o denominación es la letra, signo o secuencia de signos que define al vector.

Por lo tanto en un vector podemos diferenciar:

Nombre

Dirección

Sentido

Módulo

Punto de aplicación

Biografía de Galilei

Biografía De Galileo Galilei.

fue un astrónomo, filósofo, ingeniero, matemático y físico italiano que estuvo relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora del telescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante para el copernicanismo. Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna» y el «padre de la ciencia.

Su trabajo experimental es considerado complementario a los escritos de Francis Bacon en el establecimiento del moderno método científico y su carrera científica es complementaria a la de Johannes Kepler. Su trabajo se considera una ruptura de las teorías asentadas de la física aristotélica y su enfrentamiento con la Inquisición romana de la Iglesia católica suele presentarse como el mejor ejemplo de conflicto entre religión y ciencia en la sociedad occidental.

Biografia de Issac Newton

Biografia De Issac Newton.

fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de Philosophiae naturalis principia mathematica, más conocidos como los Principia, donde describió la ley de la gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks) y el desarrollo del cálculo matemático.

Newton comparte con Leibniz el crédito por el desarrollo del cálculo integral y diferencial, que utilizó para formular sus leyes de la física. También contribuyó en otras áreas de la matemática, desarrollando el teorema del binomio y las fórmulas de Newton-Cotes.

Entre sus hallazgos científicos se encuentran el descubrimiento de que el espectro de color que se observa cuando la luz blanca pasa por un prisma es inherente a esa luz, en lugar de provenir del prisma (como había sido postulado por Roger Bacon en el siglo XIII); su argumentación sobre la posibilidad de que la luz estuviera compuesta por partículas; su desarrollo de una ley de convección térmica, que describe la tasa de enfriamiento de los

Biografia de Albert Einstein

Biografia De Albert Einstein.

fue un físico alemán de origen judío, nacionalizado después suizo y estadounidense. Es considerado como el científico más conocido y popular del siglo XX.
En 1905, cuando era un joven físico desconocido, empleado en la Oficina de Patentes de Berna, publicó su teoría de la relatividad especial. En ella incorporó, en un marco teórico simple fundamentado en postulados físicos sencillos, conceptos y fenómenos estudiados antes por Henri Poincaré y por Hendrik Lorentz. Como una consecuencia lógica de esta teoría, dedujo la ecuación de la física más conocida a nivel popular: la equivalencia masa-energía, E=mc². Ese año publicó otros trabajos que sentarían bases para la física estadística y la mecánica cuántica.
En 1915 presentó la teoría de la relatividad general, en la que reformuló por completo el concepto de gravedad.Una de las consecuencias fue el surgimiento del estudio científico del origen y la evolución del Universo por la rama de la física denominada cosmología. En 1919, cuando las observaciones británicas de un eclipse solar confirmaron sus predicciones acerca de la curvatura de la luz, fue idolatrado por la prensa. Einstein se convirtió en un icono popular de la ciencia mundial mente famoso, un privilegio al alcance de muy pocos científicos.

Unidades basicas

En política argentina se denomina unidad básica al ámbito físico donde concurren militantes peronistas para realizar distintas actividades. Su origen se remonta al nacimiento del justicialismo.

Su función es ser el lugar de reunión donde se tratan los asuntos partidarios y comunales así como formar cuadros políticos. En sus comienzos también servían como lugar de instrucción pública donde se aprendía a leer y escribir, se leían libros y también se enseñaban profesiones básicas.¹ Cada unidad puede tener un nombre propio y es usual que existan varias por ciudad.

Movimiento circular uniforme

En física, el movimiento circular uniforme (también denominado movimiento uniformemente circular) describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.

Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.

Movimientos del MCU 

-Frecuencia

-Periodo

-Velocidad lineal

-Velocidad angular

-Aceleración centripeda 

Formulas del movimiento parabólico o lanzamiento del proyectil

1. En que consiste 
2. formula de la v.h (ux)
3. formula de la v.v (vy)
4. altura máxima 
5. tiempo de vuelo 
6. recorrido o alcance máximo 
7. para que angulo el alcance es máximo 

                                                           SOLUCIÓN 

1. El movimiento parabólico es aquel cuya ruta de lanzamiento produce un arco al terminar, comienza con un lanzamiento horizontal. con un grado de inclinación, también dicho lanzamiento tendrá una fuerza inicial la cual junta con la inclinación le dará la distancia máxima de recorrido, llegando a un punto critico donde ya no subirá en altura si no que bajara debido a que la fuerza inicial sera igual a cero y desendera por pura gravedad  Ejemplo:  el tiro de un de fútbol americano puede ser analizado como la composición de dos movimientos rectilíneo : un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical


2.  Formula velocidad horizontal  (Vx)
Vx = Vo. Cos θ


3.  Formula velocidad vertical 
Vy = Vo . Sen θ - g.t

4.  Altura máxima : La altura maxima que alcanza un proyectil se obtiene con Vy = 0
su valor máximo se obtiene para el angulo de disparo θ-90°



5. Tiempo de vuelo: El tiempo de vuelo en tiro parabólico, siempre que el piso sea horizontal, esto dado por:
 Tr: 2(vo/g) senθ donde vo es la velocidad inicial, g la aceleración de la gravedad y θ el angulo de elevación, que es lo mismo que el angulo que forma la velocidad inicial respecto a la horizontal.


6.  Recorrido o alcance máximo: El alcance máximo lo encontramos con : 2Vo. Cos θ/g.


7. Angulo con alcance máximo : El alcance máximo se obtiene para el angulo de tiro, 45° cuando el caño y el blanco están en una superficie horizontal.
su valor máximo se obtiene para un angulo  θ =45° teniendo el mismo valor para θ = 45 +4, que para  θ = 45-9

Sistema fisico

Se define un sistema físico como cualquier porción de materia. en todo sistema es posible definir unos limites, entre lo que esta afuera de este. De esta manera, un sistema es también la materia y la energía que entra y sale de el Ejemplo: una estrella, un átomo de cualquier elemento, un resorte, el sistema tierra luna o un montaje experimental.

las relaciones del sistema con su entorno son sumamente importantes para la descripción completa del mismo. por ejemplo, si consideramos el sistema físico formado por un recipiente que contiene agua la influencia de la temperatura del medio que lo rodea puede provocar que el agua hierva o que por el contrario se congele

Movimiento semiparabolico

El movimiento de parábola o semiparabólico (lanzamiento horizontal) se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre de un cuerpo en reposo.


El movimiento semiparabolico es el movimiento horizontal que realizan diferentes objetos, el ejemplo más claro de este movimiento es el lanzamiento de un proyectil, parte con una velocidad 0. 

Caída libre

En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.

El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como undisparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.

Formula :     

1)Distancia es igual a Velocidad final menos Velocidad inicial .. eso entre dos y luego por el tiempo 
s = ((Vf - Vo) /2) (t) 

2)Velocidad final es igual a Velocidad inicial más... gravedad por tiempo. 
Vf = Vo + gt 

3)Velocidad final al cuadrado es igual a ... Velocidad inicial al cuadrado... más gravedad por distancia por 2.. 

Vf^2 = Vo^2 + gs2 

4) Velocidad inicial por el tiempo más la mitad de la gravedad por el tiempo al cuadrado 

s = Vot + 1/2 gt^2 

Movimiento uniformemente acelerado (M.U.R)

  Gratificas :

                               

Formulas :  

                          

Formulas y gráficas del M.R.U

Formulas : A partir de las siguientes relaciones obtenemos todas las formulas: 
a = dv/dt => a*dt = dv 
v = dx/dt => v*dt = dx 
Integras con extremos generales (t,to o x,xo y v,vo) para que sea válido en cualquier instante. 

Ahora para el Movimiento Rectilíneo Uniforme (MRU), donde el movimiento es en una direccion y la velocidad constante: 
- Ecuacion de posicion: X = Xo + Vt, donde: 
X = Posicion final 
Xo = Posicion inicial 
V = Velocidad (constante). 
t = Tiempo 

Para el Movimiento Rectilineo Uniformemente variado (MRUV), donde está acelerado (velocidad varia uniformemente) : 
- Ecuacion de posicion: X = Xo + Vot + 1/2*a*t^2 

- Ecuación de velocidad: V = Vo + at , donde: 

a = aceleracion (constante) 
V = Velocidad final 
Vo = Velocidad inicial 

Gráficas : 

Velocidad vs tiempo 

Elementos del movimiento

1.    Movimiento
Es el cambio de posición que experimenta un cuerpo respecto a un sistema de referencia al transcurrir el tiempo.

2.    La Posición Inicial y Final
Nos indica que el cuerpo es estudiado en determinados instantes, esto quiere decir que el movimiento del cuerpo posee diferentes posiciones a lo largo de la trayectoria

3.    Trayectoria
Es la línea discontinua recta o curva que recorre el móvil durante su movimiento. Dicho de otra manera, es el camino que describe el móvil.

4.    Espacio (e)
Denominado también recorrido, se denomina así a la longitud, valor o medida de la trayectoria.

5.    Vector desplazamiento 
Es un vector que nos une la posición inicial y final

6.    Distancia (d)
Es el valor o medida del vector de desplazamiento

7.    Móvil
Es el cuerpo que realiza el movimiento

8.    Velocidad (V)
Es una magnitud vectorial que mide el espacio recorrido por el móvil en cada unidad de tiempo, su dirección es tangente a la trayectoria y su sentido es el mismo que el del movimiento del cuerpo. Se denomina rapidez al módulo de la velocidad. Su unidad en el SI es el m/s.

9.    Rapidez
Es el valor o medida de la velocidad

Representación de un vector

la dirección de l vector debe coincidir con la dirección de la recta que lo contiene  ya que un vector se representa por medio de un segmento dirigido por la recta.
por ,o tanto la dirección del vector nos lo da el angulo. el sentido de un vector lo indica la flecha.
el valor numérico, magnitud o modulo queda representando por la longitud de la recta, las características de un vector son : magnitud , dirección y sentido anteriormente definida

Magnitudes

Magnitudes escalares : son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Esto es, las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo, pero que carecen de dirección. Su valor puede ser independiente del observador (v.g.: la masa, la temperatura, la densidad, etc.) o depender de la posición (v.g.: la energía potencial), o estado de movimiento del observador (v.g.: la energía cinética).



Magnitudes vectoriales : son aquellas que quedan caracterizadas por una cantidad (intensidad o módulo), una dirección y un sentido. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa mediante un segmento orientado. Ejemplos de estas magnitudes son: la velocidad, la aceleración, la fuerza, el campo eléctrico,intensidad luminosa, etc. Además, al considerar otro sistema de coordenadas asociado a un observador con diferente estado de movimiento o de orientación, las magnitudes vectoriales no presentan invariancia de cada uno de los componentes del vector y, por tanto, para relacionar las medidas de diferentes observadores se necesitan relaciones de transformación vectorial. En mecánica clásica también el campo electrostático se considera un vector; sin embargo, de acuerdo con la teoría de la relatividad esta magnitud, al igual que el campo magnético, debe ser tratada como parte de una magnitud tensorial.



Magnitudes tensoriales : son las que caracterizan propiedades o comportamientos físicos modelizables mediante un conjunto de números que cambian tensorialmente al elegir otro sistema de coordenadas asociado a un observador con diferente estado de movimiento (marco móvil) o de orientación.

De acuerdo con el tipo de magnitud, debemos escoger leyes de transformación (por ej. la transformación de Lorentz) de las componentes físicas de las magnitudes medidas, para poder ver si diferentes observadores hicieron la misma medida o para saber qué medidas obtendrá un observador, conocidas las de otro cuya orientación y estado de movimiento respecto al primero sean conocidos.